Loss functions - Categorical Cross Entropy
Understanding Softmax and negative log loss
In categorical cross entropy our convolutions result in an output for each category with the highest value for the predicted category. That is given we have 5 categories
- cat
- dog
- plane
- fish
- building
Our loss function, Categorical Cross Entropy (in the case of Multiclass classification), is made up of the following steps with the predictions. The following sections describe what actually happens at each of these steps.
- Softmax
- Negative log” loss
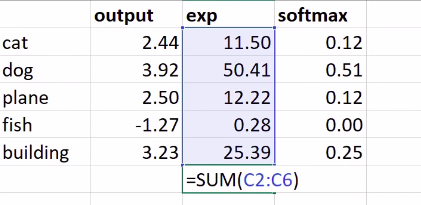
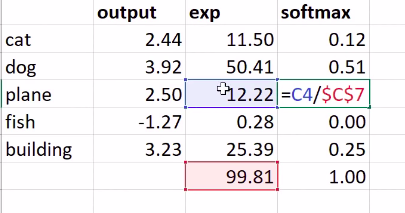
Before we jump into Softmax it makes sense to have a grasp of how we arrived at these predictions. How did the convolutions yield a Tensor of shape $(50000, 10)$. A quick overview is available here
Softmax
if our predictions are
# Our predictions as a result of the model.
pred_tensor = torch.Tensor([2.44, 3.92, 2.50, -1.27, 3.23])
#tensor([ 2.4400, 3.9200, 2.5000, -1.2700, 3.2300])
pred_tensor.exp()/(pred_tensor.exp().sum())
#Softmax is tensor([ 2.4400, 3.9200, 2.5000, -1.2700, 3.2300])
Assuming $x_i$ represents a activation from a layer.
\[\hbox{softmax(x)}_{i} = \frac{e^{x_{i}}}{e^{x_{0}} + e^{x_{1}} + \cdots + e^{x_{n-1}}}\]To compute the loss we need the log of softmax.
# Keep dim in the `sum` simply retains the rank 1 dimension we had for `pred_tensor` instead of returning a scalar
(pred_tensor.exp()/(pred_tensor.exp().sum(-1, keepdim=True))).log()
#tensor([-2.1613, -0.6813, -2.1013, -5.8713, -1.3713])
Now given our model and a log softmax function are as follows. Ignore the placeholder MSELoss used in the code.
class Model(nn.Module):
def __init__(self, n_in, nh, n_out):
super().__init__()
self.layers = [
nn.Linear(n_in, nh),
nn.ReLU(),
nn.Linear(nh, n_out)
]
self.loss = nn.MSELoss()
def __call__(self, x, targ=None):
for l in self.layers:
x = l(x)
print(f'Shape of x during iterations {x.shape}')
print(x.shape, x.squeeze().shape)
#_loss = self.loss(x.squeeze(), targ)
return x
def log_softmax(preds):
return (preds.exp()/(preds.exp().sum(-1, keepdim=True))).log()
# negative log loss
def nll(sm_preds, target):
return -sm_preds[range(target.shape[0]), target].mean()
If we pass in our inputs we get 10 predictions for each of our 50K inputs so our output shape for preds is $50000,10$
Now we obtain the possible predictions for input 0, 1 and 2
def get_data():
path = datasets.download_data(MNIST_URL, ext='.gz')
with gzip.open(path, 'rb') as f:
((x_train, y_train), (x_valid, y_valid), _) = pickle.load(f, encoding='latin-1')
return map(tensor, (x_train, y_train, x_valid, y_valid))
x_train, y_train, x_valid, y_valid = get_data()
n,m = x_train.shape
c = y_train.max()+1
nh = 32
model = Model(m, nh, c)
preds = model(x_train)
sm_preds = log_softmax(preds)
sm_preds[0,1,2]
Negative Log Loss
Is the negative log of the probability of a prediction x.
\[- \sum x\, \log p(x)\]For one hot encoded it’s
\[- \log p_{i}\]We’ve already computed the log in the softmax function so we compute the negative value for the probability of a specific value.
For example, here is something our model returned for the x_train input.
sm_preds=log_softmax(preds);sm_preds
# tensor([[ 0.2030, -0.0639, 0.0886, 0.0786, -0.2448, 0.0354, -0.0219, -0.0123,
# -0.1520, 0.2039],
# [ 0.2311, -0.0703, 0.0598, 0.0556, -0.2017, -0.0300, -0.0216, 0.0413,
# -0.1391, 0.1339],
# [ 0.2227, -0.1736, 0.0950, -0.0588, -0.1586, 0.0774, -0.0949, -0.0062,
# -0.2034, 0.2546]], grad_fn=<SliceBackward>)
sm_preds.shape
# torch.Size([50000, 10])
sm_preds[0:3]
<!-- tensor([[-2.1202, -2.3871, -2.2346, ..., -2.3355, -2.4752, -2.1193],
[-2.0846, -2.3861, -2.2560, ..., -2.2745, -2.4548, -2.1819],
[-2.0874, -2.4837, -2.2151, ..., -2.3163, -2.5135, -2.0555],
...,
[-2.0787, -2.3651, -2.2467, ..., -2.3303, -2.4289, -2.2740],
[-2.0677, -2.4694, -2.3126, ..., -2.2843, -2.4449, -2.1239],
[-2.0931, -2.4160, -2.1421, ..., -2.3069, -2.5062, -2.1928]],
grad_fn=<LogBackward>) -->
This is essentially the probabilities of our input with respect to one of the 10 possible output categories. 1 to 10 in this case since it’s MNIST (0 to 9 as indexes or categories)
The training set category for input row 0 is category 5.
y_train[0]
#tensor(5)
With Negative log loss we’re computing
- for each record in
sm_predsobtain the probability of the relevanty_traincategory. This simply returns a tensor of size 50000 containing the probabilities of each of the expected category for all the elements insm_predswhich is our softmax predictions list
sm_preds[range(y_train.shape[0]), y_train]
- We compute the mean and return the negative of the value as the
negative log loss. Therefore
def nll(sm_preds, target):
return -sm_preds[range(target.shape[0]), target].mean()
So now our loss can be defined as
loss = nll(sme_preds, y_train)
Using Pytorch’s implementation
1. Softmax
from torch.functional import F
F.log_softmax(preds, -1)
# tensor([[-2.1662, -2.3965, -2.3194, ..., -2.1961, -2.1526, -2.2869],
# [-2.2161, -2.3494, -2.3951, ..., -2.1872, -2.1880, -2.2755],
# [-2.1842, -2.3952, -2.4618, ..., -2.1759, -2.2801, -2.3158],
# ...,
# [-2.1914, -2.4641, -2.3243, ..., -2.2016, -2.2357, -2.2430],
# [-2.2377, -2.4174, -2.4349, ..., -2.1115, -2.1685, -2.2680],
# [-2.2135, -2.4548, -2.3279, ..., -2.1169, -2.2617, -2.3048]],
# grad_fn=<LogSoftmaxBackward>)
View the shape
F.log_softmax(preds, -1).shape
#torch.Size([50000, 10])
Negative log loss
F.nll_loss(F.log_softmax(preds, -1), y_train)
#tensor(2.3115, grad_fn=<NllLossBackward>)
Pytorch provides a convenience method
F.cross_entropy(preds, y_train)
#tensor(2.3115, grad_fn=<NllLossBackward>)
from torch import nn;
from torch.functional import F
F.log_softmax(preds, -1).shape
F.nll_loss(F.log_softmax(preds, -1), y_train)
F.cross_entropy(preds, y_train)
tensor(2.3115, grad_fn=<NllLossBackward>)