Softmax - Why does the classifier say an image contains a category when it actually doesn’t
This is something I struggled to understand when i started building my first classifiers and it deals with understanding what softmax actually does.
One of the things I ended up doing was introducing noise in the form of categories I wanted the classifier to ignore which in turn affected the accuracy.
Softmax
The job of is to predict if one of the categories is present in the input image. However, softmax will return a likelihood for each category’s presence in the image. So it’s easy to assume the category with the highest value is present in the image. However, we know that’s not true.
Since we know softmax is
\[\hbox{softmax(x)}_{i} = \frac{e^{x_{i}}}{e^{x_{0}} + e^{x_{1}} + \cdots + e^{x_{n-1}}}\]It’s always going to add up to 1.
The presence of a category can be determined by using a binary approach instead.
\[b=\frac{e^x}{1+e^x}\]to determine if the category is actually present and is more representative of the ground truth.
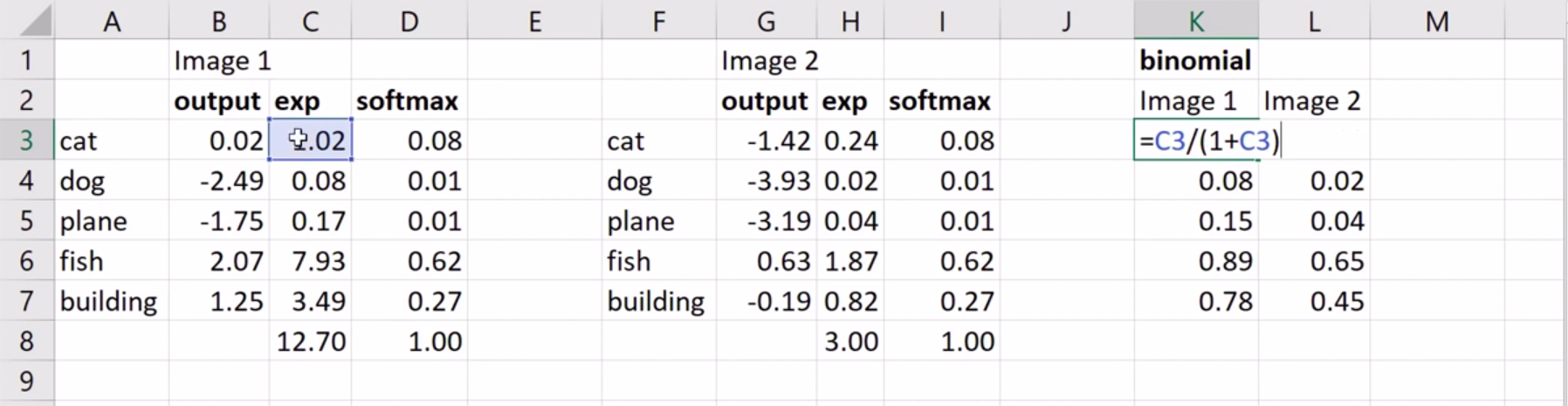
The heading in the image that reads binomial actually means binary derived from “multi label binary classification” and is the approach used in multi label classification. This discussion is a useful thread on how to change the loss function to use BCE instead of categorical_cross_entropy
Understanding the image:
- Image1, indicates via softmax that the category is most likely a fish, with a possibility of a building in the image.
- For image 2, while the activations are significantly different but the softmax computation seems to be identical to image1
The binary approach provides more clarity into what could actually be present.
- Image1 says that there could be a fish along with a building and possibly a cat.
- Image2 could possibly have a a fish in it but it but we can’t be certain about anything.
Categorical Cross Entropy and Binary Cross Entropy
While fundamentally both functions behave the same, that is, they both are the sum of the negative log loss of some function $f(x)$. The function is what determines how they differ.
Here $t$ is the target value being and $s$ indicates the score generated by our activation in a one hot encoded category list.
In the case of Categorical Cross Entropy which is usually used in MultiClass classification, the function used is softmax which ensures the values of the activation are within the range 0 and 1 and add up to 1. But here the values of each score depends on the values of the other categories in our list of categories. Hence it’s the negative log loss of softmax.
In the case of Binary Cross Entropy which is used in MultiLabel classification, the function used is sigmoid which also ensures the activations are within the range of 0 and 1 but does not add up to 1. Thus our outputs aren’t dependent on each other. Given, we want to independently assess if our image contains 2 different classes. That is, does it contain a cat and a dog.
So in the case of BCE our $f(s)$ is
\[b=\frac{e^x}{1+e^x}\]and our $CE$ is
\[CE = -\sum_{i=1}^{C'=2}t_{i} log (f(s_{i})) = -t_{1} log(f(s_{1})) - (1 - t_{1}) log(1 - f(s_{1}))\]